抽象函数与 Banach 代数--大纲
私以为这课叫 Banach 代数与 C *代数也挺好(哈哈哈哈
Part1 Banach 代数
Banach 代数的定义:代数,满足范数不等式(若有单位元,则要求?\(\|\mathbb{1}\|=1\)) ------ 2021.09.09 L1
- 例子:
- 复数域
- 连续函数空间\(C(\Omega)\),其中\(\Omega\) 为紧 Hausdorff 空间
- \(B(X)\) Banach 空间 X 上的有界线性算子全体
- \(B(\mathbb{C}^n) \cong M_{n\times n}(\mathbb{C})\)
- \(l_1(\mathbb{Z})\),乘法定义为卷积
- 商 Banach 代数
- \(l_{\infty}/c_0\)
- Calkin 代数:\(B(H)/K(H)\)
- 例子:
可逆元
- \(\mathbb{1}-x\) 可逆,若\(\|x\| \leqslant 1\)
- 全体\(G(A)\)为开集 ------ 2021.09.16 L2
- 逆运算连续,故为\(G(A)\)上的同胚
谱\(\sigma(x)\)、预解集\(\rho(x)\)、谱半径\(r(x)\)
- 例子:
- 矩阵:特征值
- \(C(\Omega)\):函数值(图像)
- 无限维空间中,谱不一定有对应的“特征向量”!
- 对 Banach 代数,谱集为非空紧集
- 非空的证明很有趣,构造了一个全纯函数,用 Liouville 定理来证明它为常数(0)导出矛盾
- Cor: Banach 代数+可除代数(任意非零元均可逆)\(\Rightarrow\) 等距同构于\(\mathbb{C}\)
- 谱半径不大于模长:\(r(x)\leqslant \|x\|\)
- \(\mathbb{1}-xy\) 可逆 \(\Leftrightarrow\) \(\mathbb{1}-yx\) 可逆
- Cor: \(\sigma(xy)\cup \{0\} = \sigma(yx)\cup \{0\}\), \(r(xy)=r(yx)\)
- 例子:
弱拓扑与弱*拓扑
- 定义略
- 网
- Alaoglu 定理:对偶空间的单位闭球在弱 * 拓扑下是紧集,即\((B_1(X^*), W^*)\)是紧集 ------ 2021.09.23 L3
- 记 \(\Omega = (B_1(X^*), W^*)\),则 Banach 空间 X 在典则映射\(\phi\)下线性等距同构于\(C(\Omega)\)的闭子空间。
- 对于 Banach 代数,我们希望改善\(\Omega\)使得\(\phi\)也保持乘法,即\(\phi(xy) = \phi(x) \phi(y)\),不难知道这即需将\(\Omega\)替换为保乘函数构成的空间
保乘线性泛函、极大理想空间、Gelfand 变换
- 保乘线性泛函\(\varphi\)
- 是有界线性泛函,且\(\|\varphi\| = 1\)
- 保乘线性泛函全体\(M_A\)是\(B_1(A^*)\)在\(W^*\)拓扑下的闭子集,从而紧,\((M_A,W^*)\)为紧 Hausdorff 空间
- Gelfand 变换:$: A C(M_A,W^*),; (x)() = (x) $
- 保乘法,\(\|\Gamma\| = 1\),为有界线性同态
- 极大理想空间 ------ 2021.09.30 L4
- 非平凡保乘线性泛函与 A 中极大理想一一对应(A 交换),因此称\(M_A\)为极大理想空间
- \(\varphi \leftrightarrow \ker (\varphi)=I\),反方向的证明比较有趣
- 注意极大理想一定是真理想!因此平凡的保乘线性泛函 0 不能加进来
这玩意跟 Affine variety 有点像诶(Hilbert's Nullstellensatz)
- A 为交换 Banach 代数,则 x 在 A 中可逆\(\iff\)\(\Gamma(x)\)在\(C(M_A,W^*)\)中可逆,从而\(\sigma_A(x) = \sigma_{C(M_A)}(\Gamma(x)) = Range(\Gamma(x))\) 用到 Zorn 引理
- A 为 Banach 空间,\(x, y \in A,\; xy=yx\),则\(\sigma(x+y) \subset \sigma(x) + \sigma(y),\; \sigma(xy) \subset \sigma(x)\sigma(y)\)
- 证明:构造包含 x,y 的交换 Banach 子代数
- 注意:$B A _B(x) _A(x),; _B(x) _A(x) $
- 谱映射定理:A 为 Banach 代数,$x A $, \(f(z)\) 在\(|z| \leqslant \|x\|\) 上解析,则 $(f(x)) = f((x)) $
- 证明方法同上
- A 为 Banach 空间,\(x, y \in A,\; xy=yx\),则\(\sigma(x+y) \subset \sigma(x) + \sigma(y),\; \sigma(xy) \subset \sigma(x)\sigma(y)\)
- 非平凡保乘线性泛函与 A 中极大理想一一对应(A 交换),因此称\(M_A\)为极大理想空间
- 对交换 Banach 代数 A,Gelfand 变换\(\Gamma\)是等距\(\iff\) \(\|x\| = r(x),\; \forall x \in A\) \(\iff\) \(\|x^2\| = \|x\|^2,\; \forall x \in A\) ------ 2021.10.09 L5
- 证明:谱半径公式:\(r(x) = \lim\limits_{n \to \infty} \|x^n\|^{\frac{1}{n}}\)
- 保乘线性泛函\(\varphi\)
Gelfand 变换的例子
- 盘代数\(A(\mathbb{D})\)为在\(\bar{\mathbb{D}}\)上解析,在\(\partial{\mathbb{D}}\)上解析的函数全体
- 由于 \(\bar{\mathbb{D}}\) 到\(M_{A(\mathbb{D})}\) 有满同胚,故 Gelfand 变换\(\Gamma : A(\mathbb{D}) \to C(M_{A(\mathbb{D})}) \leftrightarrow C(\bar{\mathbb{D}})\)为恒等映射。
- 连续函数空间\(C(K)\)
- 由于 \(K\) 到\(M_{C(K)}\) 有满同胚,故 Gelfand 变换\(\Gamma : C(K) \to C(M_{C(K)}) \leftrightarrow C(K)\)为恒等映射。
- \(l^1(\mathbb{Z})\),乘积为卷积------ 2021.10.14 L6
- 由于 \(M_{l^1(\mathbb{Z})}\) 到 \(\partial{\mathbb{D}}\) 有满同胚,故 Gelfand 变换\(\Gamma : l^1(\mathbb{Z}) \to C(M_{C(l^1(\mathbb{Z}))}) \leftrightarrow C(\partial{\mathbb{D}})\)为恒等映射。
- 盘代数\(A(\mathbb{D})\)为在\(\bar{\mathbb{D}}\)上解析,在\(\partial{\mathbb{D}}\)上解析的函数全体
非单位 Banach 代数
- 例子:
- \(c_0,\;C_0(\mathbb{R})\)
- 无限维 Banach 空间上的紧算子全体\(K(X)\)
- \(L^1(\mathbb{R})\),乘积为卷积
- 单位化:直和上一个\(\mathbb{C}\),并定义恰当的乘法和范数
- 基本性质(大多靠单位化之后的空间推出)
- 保乘线性泛函是有界线性泛函,且\(\|\varphi\| \leqslant 1\)(无法保证取等!)
- \((M_A,W^*)\)为局部紧 Hausdorff 空间
- Gelfand 变换:\(\Gamma : A \to C_0 (M_A)\)为保乘有界线性同态,且\(\|\Gamma\| \leqslant 1\)
- 极大理想空间:对局部紧 Hausdorff 空间\(\Omega\),有极大理想空间\(M_{C_0(\Omega)} \cong \Omega\),从而 Gelfand 变换\(\Gamma\)为恒等映射:\(C_0(\Omega) \to C(M_{C_0(\Omega)})\)
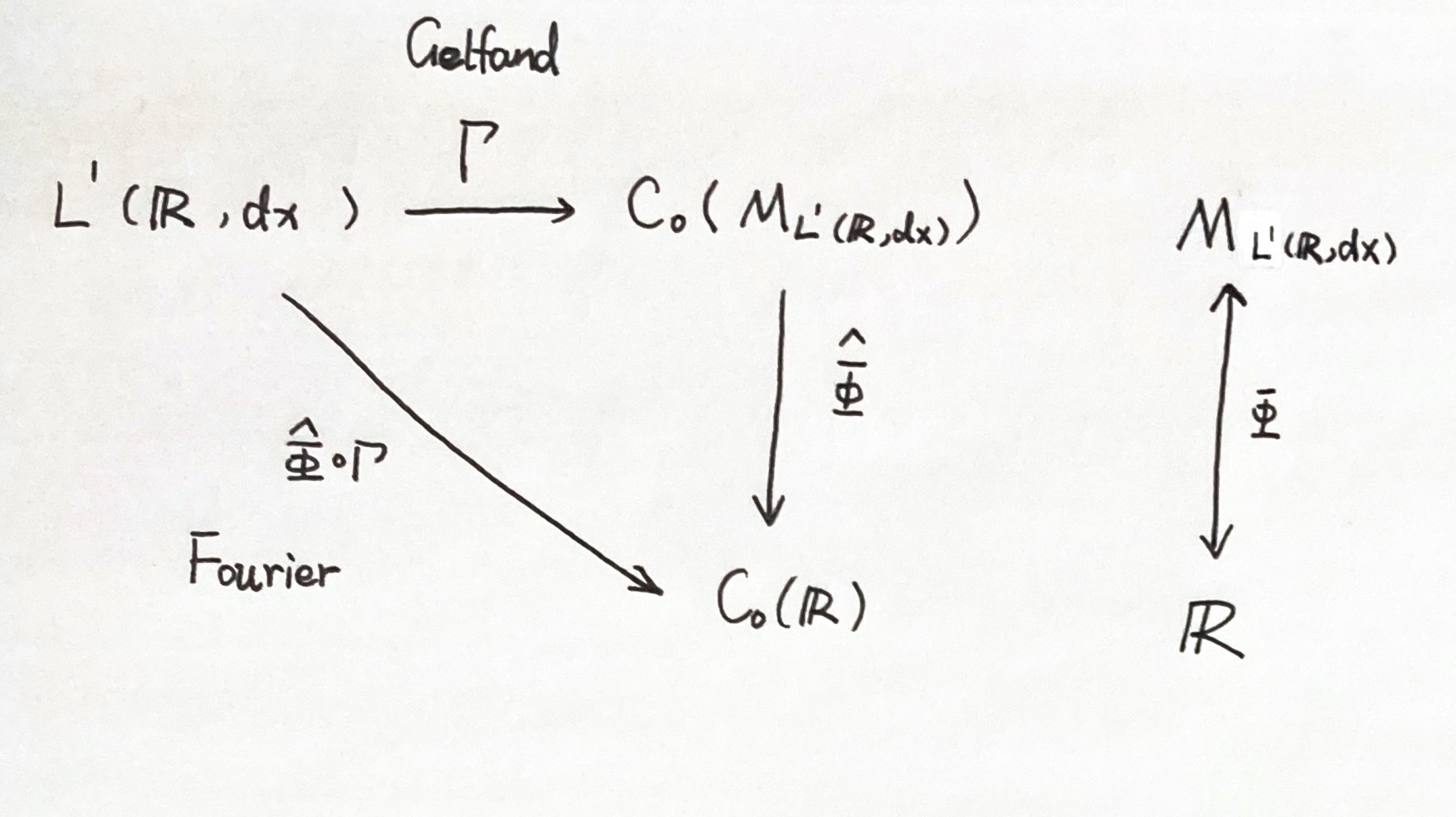
- 例子:\(L^1(\mathbb{R})\),乘积为卷积;此时 Gelfand 变换配合上述同胚即 Fourier 变换(这里不太好表述,见下图)------ 2021.10.21 L7
- 例子:
Part 2 \(C^*\)代数
\(C^*\)代数定义
- 例子
- \(\mathbb{C}\)
- \(C(K)\),其中 K 为紧 Hausdorff 空间
- 复\(M_{n \times n}\)
- \(B(H)\),H 为 Hilbert Space
- \(C^*\)代数的子代数也是\(C^*\)代数
- 例子
自伴、酉元、正规、正、投影元
1
2
3
4
5graph TD
正元-->自伴;
自伴-->正规;
投影-->自伴;
酉元-->正规;
正规,则\(r(x) = \|x\|\)
- 从而对任意 x,\(\|x\|=\sqrt{\|x^*x\|}=\sqrt{r(x^*x)}\)
x 自伴\(\implies \sigma(x) \subset \mathbb{R}\)
x 酉元\(\implies \sigma(x) \subset \partial D\),这里 D 为单位开圆盘
\(C^*\)同态 ------ 2021.10.28 L8
\(C^*\)同态范数为 1
\(C^*\)同态+单射=\(C^*\)同构
\(C^*\)同构为等距(因可逆性完全一致,谱集对应,范数等价)
交换\(C^*\)代数的表示:交换\(C^*\)代数 A 同构与\(C(K)\),K 为某紧 Hausdorff 空间(此即 Gelfand 变换,\(K=M_A\)) 有以下推论:(交换情况)
- x 自伴 \(\iff \sigma(x) \subset \mathbb{R}\)
- x 酉元 \(\iff \sigma(x) \subset \partial D\)
- x 为正元 \(\iff \sigma(x) \subset \mathbb{R}^+ \cup {0}\)
- x 为投影元 \(\iff \sigma(x) \subset \{0,1\}\)
例子:
证明$M_{L^{} ()} $ 为极端不连通的紧 Hausdorff 空间 ------ 2021.11.04 L9
若\(C^*\)子代数 B 继承\(C^*\)代数 A 的单位元,B 中元的可逆性与 A 中元的可逆性等价,从而\(\sigma_B (x) = \sigma_A (x)\)
谱定理:对正规元 x,\(A [x]\)的极大理想空间同胚于\(\sigma(x) \subset \mathbb{C}\)
- 此时 Gelfand 变换满足 $(p(x,x^*)) = p(z,{z}) $
连续泛函演算定理: $f C((x)),; f(x) = ^{-1} (f) A [x] $ 称为连续函数演算
上述定义的 $f f(x),; C((x)) A [x] $ 为满 \(C^*\) 同构
对二元多项式 $f(z) = p(z,{z}) $ ,有 $f(x) = p(x,x^*) $ ,特别的, $ f(z) = z f(x) = x $
$(f(x)) = f((x)) $ (谱映射定理的推广!)
若 $A B $ 为 \(C^*\) 同态,则 $ f C((x)) C(((x))),; (f(x)) = f((x)) $
$f C((x)), g C((x)), $ 有 $ (g f ) (x) = g(f(x)) $
其中 d) 和 e) 证明:利用交换图 应用: ------ 2021.11.11 L10
- 推论: 有以下推论:(不需交换!)
- x 自伴 \(\iff \sigma(x) \subset \mathbb{R}\)
- x 酉元 $(x) D $
- x 为正元 \(\iff \sigma(x) \subset \mathbb{R}^+ \cup {0}\)
- x 为投影元 \(\iff \sigma(x) \subset \{0,1\}\)
- 自伴元正负部分解的存在唯一性
- 正元的平方根的存在唯一性
- Cor:\(C^*\)代数中任意元总能写成四个酉元的线性组合,或者四个正元的线性组合
- 单的\(C^*\)同态 $$ 保距离和谱集,即 $|(x) | = |x|,; ((x)) = (x) $ ------ 2021.11.18 L11
- \(C^*\)同态的像为闭集,即为\(C^*\)子代数
Hilbert 空间上算子空间\(B(H)\)
- 自伴算子
- $T B(H),; T = ( T)^{},; = (T^){} $
- T 可逆 $ T $ 在 H 中稠密,且 $,; s.t.; |Tx| |x| ; x H $ Cor: $T, T^* $ 均下有界,则 T 可逆
态(state):范 1 正泛函
注意自伴线性泛函不一定有界!但正线性泛函一定有界
$$ 自伴 \(\iff \varphi(x) \in \mathbb{R} \; \forall x\) 自伴
对自伴且有界的 $,; || = {(x) : x^*=x, |x| } $
正泛函可以达范,事实上 \(\varphi\) 为正泛函 $ $ 连续且 $ ||= () $ ------ 2021.12.02 L12
- 从而 \(\varphi\) 为态 $ $ 连续且 $ ||= () = 1 $
态空间 $S(A) $ 为 \(A^*\) 闭单位球的 $W* $ 闭凸子集
用态可以确定谱集: $x A, (x), S(A), s.t. (x) = $
- 这也说明态可以确定元的信息(GNS 构造的前提!), 即
$x=0 (x)=0 ; S(A) $
$x (x) ; S(A) $
$x (x) ; S(A) $
$x 正规 S(A), |x|=|(x)| $
GNS 构造(Gelfand–Naimark–Segal construction)
Wiki 上给的描述方式有点不一样,可以看看
- 准备工作:
- Cauchy-Schwarz 不等式:对正泛函\(\varphi\)成立\(| \varphi(x^*y) |^2 \leqslant \varphi(x^*x) \varphi(y^*y)\)
- \(\mathcal{L}_{\varphi} := \{x \in A : \varphi(x^*x) = 0 \}\) 为 A 中的闭左理想
- \(\varphi(x^*y) = 0 \Leftrightarrow x\; or\; y \in \mathcal{L}_{\varphi}\) (由 Cauchy 不等式显见)
- \(H_{\varphi}^0 := A / \mathcal{L}_{\varphi}\),定义(半)内积\(<[x], [y]> = \varphi(y^*x)\),从而\(H_{\varphi}^0\)为内积空间。\(H_{\varphi}\)为 \(H_{\varphi}^0\) 的完备化,为 Hilbert 空间。
- \(H_{\varphi}\)上的左作用算子:\(T_x: H_{\varphi}^0 \to H_{\varphi}^0,\; T_x([y]) = [xy]\),再自然延拓到 \(H_{\varphi}\) 上。
- 简单版本:
- \(\Phi : A \to B(H_{\varphi}),\; \Phi(x) = T_x\)为 C *同态
- 复杂版本:------ 2021.12.09 L13
- 一族 Hilbert 空间的直和:取可数项非零的元素。直和空间也为 Hilbert 空间,其上的有界线性泛函$T_{} \(也用直和来定义,注意所有\)T_{}$需要一致有界。
- \(\Phi : A \to B(\bigoplus\limits_{\varphi \in S(A)} H_{\varphi}),\; \Phi(x) = \bigoplus\limits_{\varphi \in S(A)} T_x^{\varphi}\)为 C *同构(直和保证了单射)
- 对于可分\(C^*\)代数 A,可以直接找到一个恰当的\(\varphi\),使得\(\Phi : A \to B(H_{\varphi}),\; \Phi(x) = T_x\)为\(C^*\)同构
非单位\(C^*\)代数
- 单位化:存在且唯一!
- 构造与证明。范数:\(\|(x,a)\| = \sup\limits_{y \in A,\; \|y\| \leqslant 1} \|xy+ay\|\)
- 谱 ------ 2021.12.16 L14
- Gelfand 变换为满的\(C^*\)同构
- 证明:从单位化的结果压回来
- 连续泛函演算:加条件\(f(0)=0\)即可
- 逼近单位元:用网来定义
- 任意非单位\(C^*\)代数有逼近单位元(实际上取的是所有模长不大于 1 的正元)
- 对于单位\(C^*\)代数也有逼近单位元:取单位元即可
- Cor: \(C^*\)代数的闭理想均有逼近单位元,从而关于\(*\)运算封闭,因此
- Cor: \(C^*\)代数的闭理想即其\(C^*\)子代数
- 在可分情况下将网改进为一个序列,则可推出有限维\(C^*\)代数必定有单位元
- 单位化:存在且唯一!
有限维 \(C^*\) 代数的表示 ------ 2021.12.23 L15
\(C^*\) 与 Kaplansky 问题 ------ 2021.12.25 L16
个人的一点点吐槽
- 感觉证明同构这样的事情做得很多,方法无外乎证明单满然后两个方向都连续
- 一般难点在于证明满射
- 已知 $f: A B $ 连续,若 A 紧,B 为 Hausdorff 空间,则 \(f\) 为同胚
Updated at 2021/12/28 09:40